Mean Field Theory of Confined Polymer Chains

Polymer chains experience a reduction in entropy when squeezed into a small space such as a narrow slit between two parallel plates or a straight narrow tube because fewer conformations are available to the repeat units in confinement than in free space. As was shown by Edwards, Doi and others, Flory’s mean-field theory can be employed to derive analytical expressions for the confinement entropy.

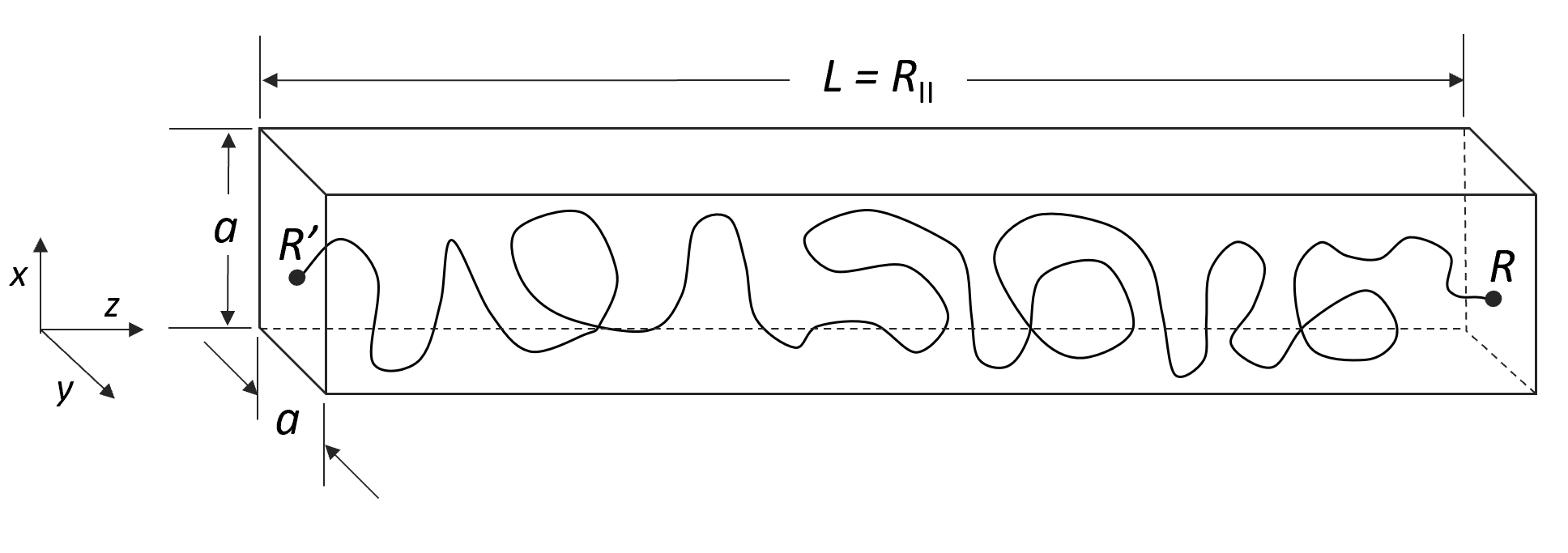
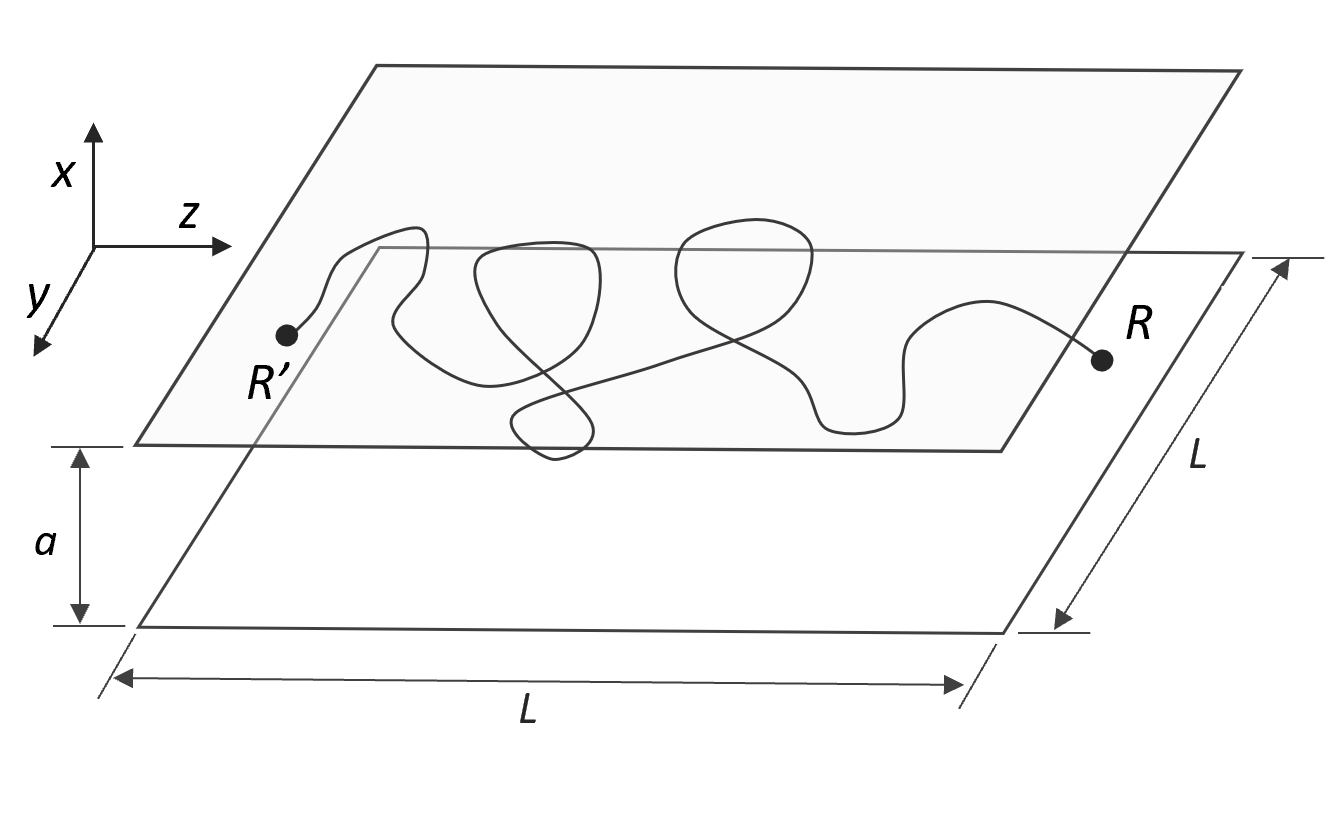
Let us consider first a polymer chain trapped in a straight tube of length L and square cross-section a². Let us further assume that the chain ends are fixed at R and R', respectively. The number of possible conformations can be calculated from the Green function, G(R,R',N). This function can be factored into three independent components G_x, G_y, and G_z,

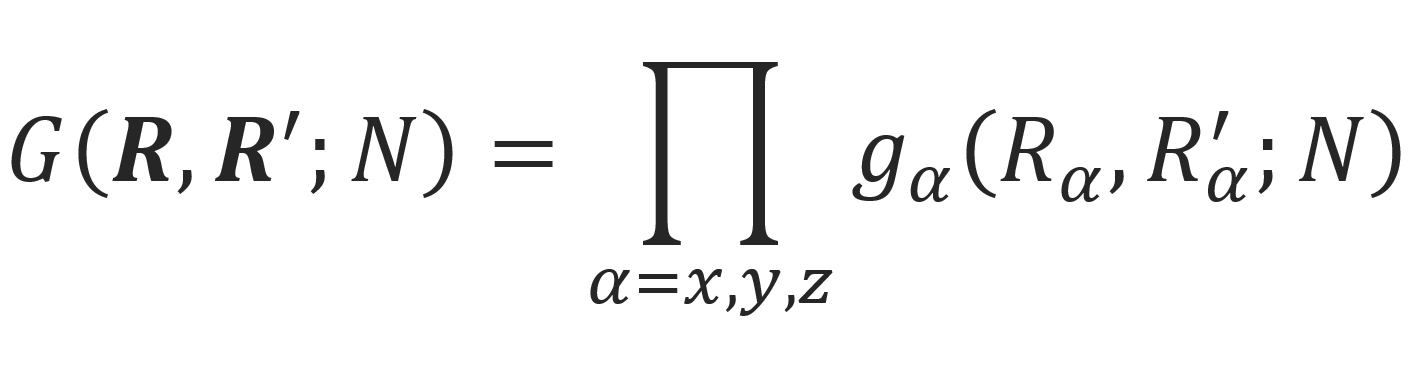
where G_z is the component of the Green function in the direction that is not restricted by a barrier, i.e. the direction parallel to the tube axes. This function is identical with the Gaussian transition probability of a one-dimensional walk:¹

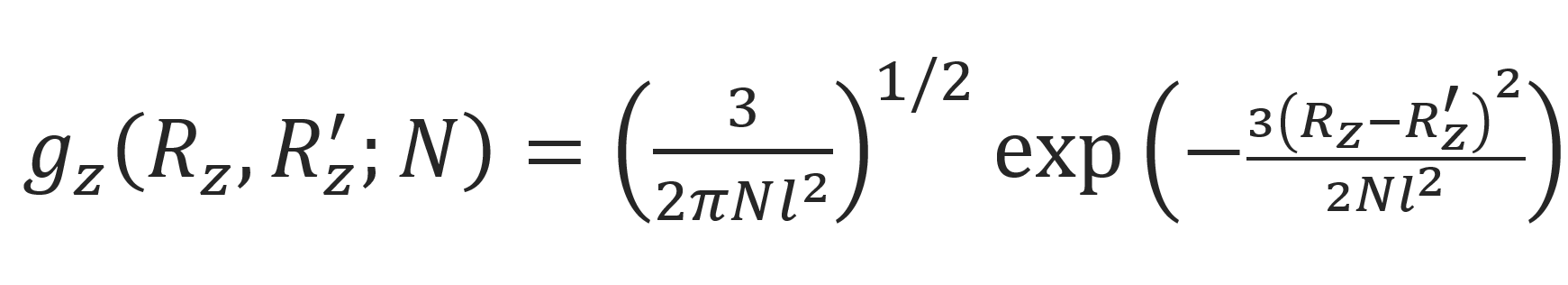
G_x and G_y have the same values since L_x = L_y = a. This function was calculated by Cassasa, Edwards, Doi and others.^2-4 It reads

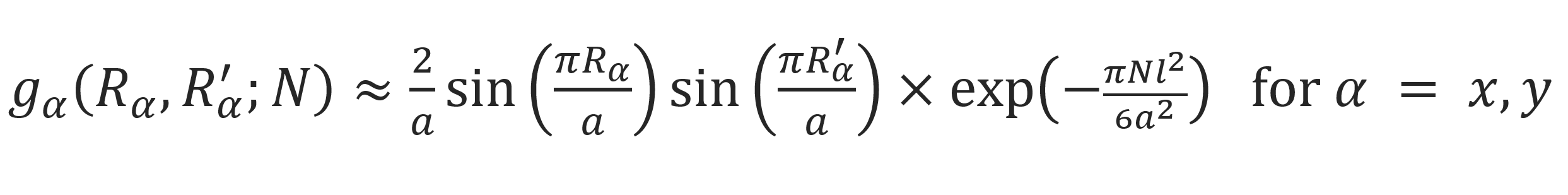
In the case of chain ends fixed at R = (a/2, a/2, L) and R' = (a/2, a/2, 0), this equation simplifies to

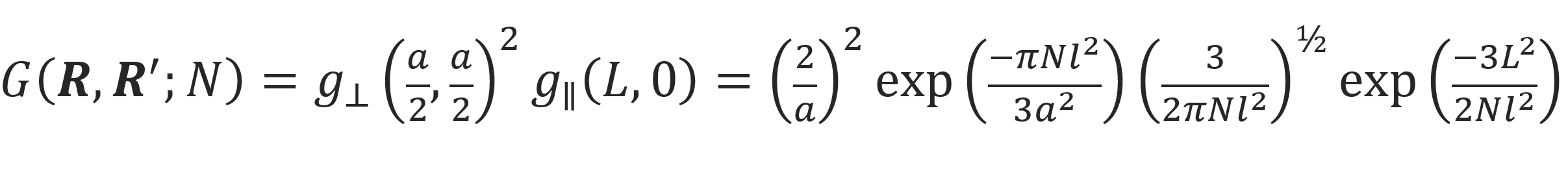
where g_⊥ and g_|| are the components of the Green function perpendicular and parallel to the pore axes, respectively.

The total number c_N of allowed conformations of the confined polymer is directly proportional to the Green function:

and the conformational entropy is obtained from:

where c_N^∞ is the number of comformations in free space. Then the entropy of a chain trapped in a tube reads

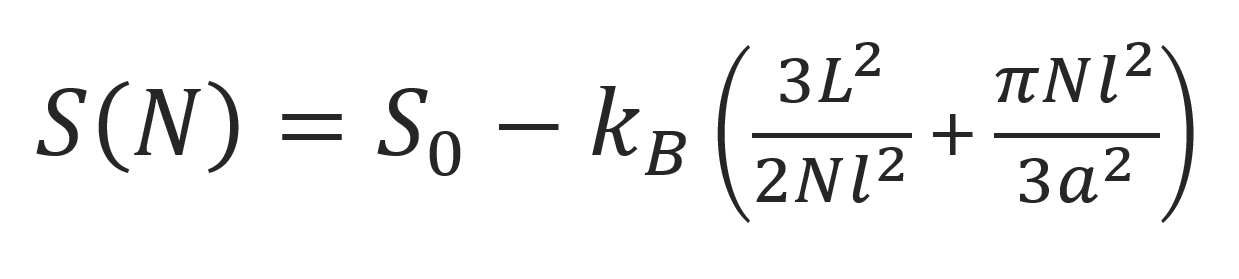
Since there is no confinement in the z directions, the chain dimension R_|| along the tube diameter is unperturbed. Then the average length in this direction is given by

In the case of a polymer trapped in a slit of width a, the polymer is confined in only one direction. Then the segment distribution parallel to the plates can be described by a Gaussian distribution. Assuming the chain ends are fixed at R = (a/2, L/2, L) and R' = (a/2, L/2, 0), a similar derivation yields

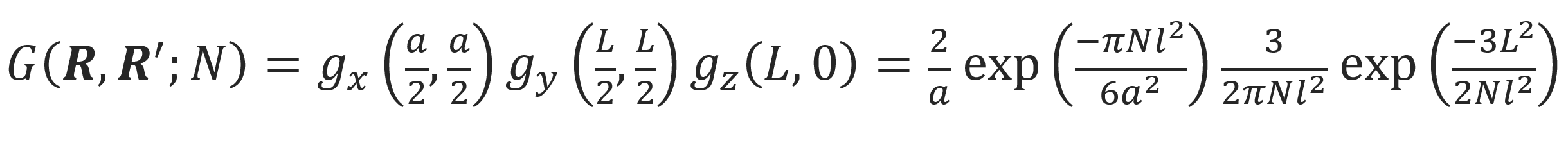
The entropy of the chain trapped in a slit is then given by

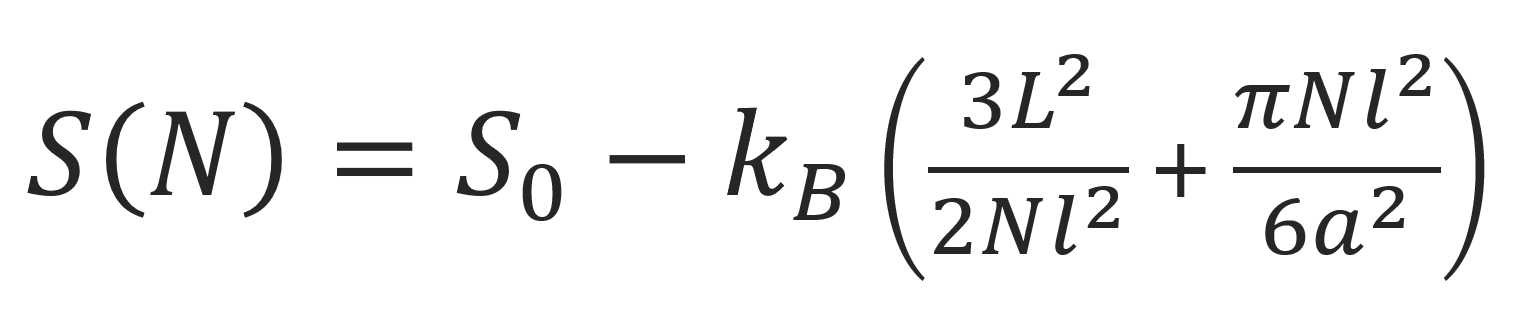
Since there is no confinement in the y and z directions, the conformations in these directions are unperturbed. Then the chain dimension R_|| along the parallel walls is given by

References & Further Readings

1. The Gaussian probability distribution can also be written in terms of of the radius of gyration, R_g:
             

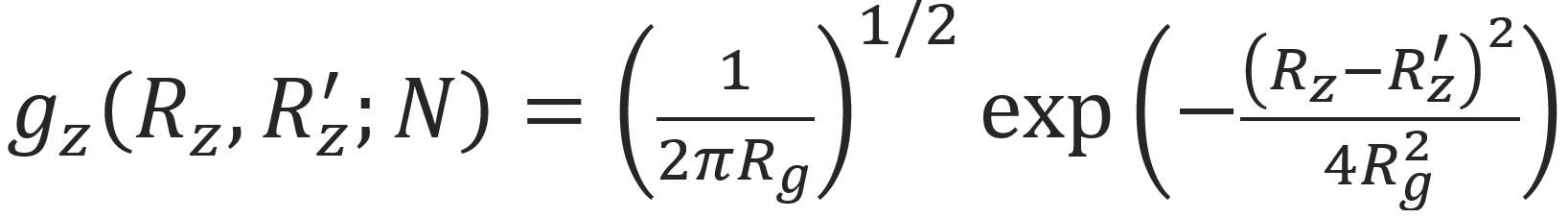
2. E.F. Casassa, J. Polym. Sci. Polym. Lett. Ed. 5, 773 (1967)

3. E. F. Casassa, Y. Tagami, Macromolecules 2, 14 (1969)

4. M. Doi, S.F. Edwards, The Theory of Polymer Dynamics, Oxford University Press, New York 1986

5. I. Teraoka, Polymer Solutions: An Introduction to Physical Properties, John Wiley (2002)

6. M. Doi, Introduction to Polymer Physics, Clarendon Press, Oxford 1995

7. P.G. de Gennes, Scaling Concepts in Polymer Physics, Cornell University Press (1970)

8. M. Rubinstein and R. Colby, Polymer Physics, 1st Ed., Oxford University Press (2003)

9. A.Y. Grosberg, A.R. Khokhlov, Statistical Physics of Macromolecules, AIP Press (1994)